红黑树和HashMap中实现

　　本人最近在看JDK的HashMap源码，在JDK1.8中引入红黑树。引入红黑树的原因是加快hash碰撞较多情景下的查找速度。网上找到下面这篇文章感觉写的非常好，思路清晰。我会在原文章基础上做一点批注，方便日后阅读。
　　

http://blog.csdn.net/eric491179912/article/details/6179908

红黑树的基本特性

　　一定要牢记这五条特性，推导全靠这几条原则。

1. 节点是红色或黑色。

2. 根节点是黑色。

3. 每个叶节点（NIL节点，空节点）是黑色的。这个限制根本没有用啊，亲 - -！

4. 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

红黑树上结点的插入

　　任何一个即将插入的新结点的初始颜色都为红色。这一点很容易理解，因为插入黑点会增加某条路径上黑结点的数目，从而导致整棵树黑高度的不平衡。但如果新结点父结点为红色时（如图1所示），将会违返红黑树性质：一条路径上不能出现相邻的两个红色结点。这时就需要通过一系列操作来使红黑树保持平衡。

　　为了清楚地表示插入操作以下在结点中使用“新”字表示一个新插入的结点；使用“父”字表示新插入点的父结点；使用“叔”字表示“父”结点的兄弟结点；使用“祖”字表示“父”结点的父结点。插入操作分为以下几种情况：

该树为空树。

直接插入根结点的位置，违反性质2，把节点颜色有红改为黑即可。

黑父

　　如图2所示，如果新点的父结点为黑色结点，那么插入一个红点将不会影响红黑树的平衡，此时插入操作完成。红黑树比AVL树优秀的地方之一在于黑父的情况比较常见，从而使红黑树需要旋转的几率相对AVL树来说会少一些。

红父

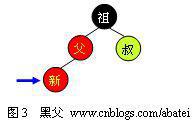
　　如图3所示，由于父结点为红色，此时可以判定，祖父结点必定为黑色。这时需要根据叔父结点的颜色来决定做什么样的操作。青色结点表示颜色未知。由于有可能需要根结点到新点的路径上进行多次旋转操作，而每次进行不平衡判断的起始点（我们可将其视为新点）都不一样。所以我们在此使用一个蓝色箭头指向这个起始点，并称之为判定点。
　　注：把一个树看成一个新的节点，继续进行旋转。这点很重要。

红叔

　　当叔父结点为红色时，如图4所示，无需进行旋转操作，只要将父和叔结点变为黑色，将祖父结点变为红色即可。但由于祖父结点的父结点有可能为红色，从而违反红黑树性质。此时必须将祖父结点作为新的判定点继续向上进行平衡操作。需要注意，无论“父”在“叔”的左边还是右边，无论“新”是“父”的左孩子还是右孩子，它们的操作都完全一样。

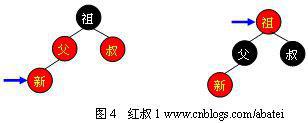
　　注：如果祖父节点是根节点怎么办？答案是进行情景一的操作，把祖父节点变为黑色。

黑叔

情形1：

情形2：

情形3：

情形4：

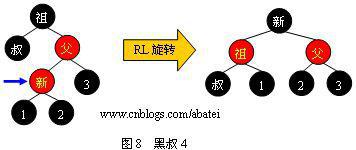
　　可以观察到，当旋转完成后，新的旋转根全部为黑色，此时不需要再向上回溯进行平衡操作，插入操作完成。需要注意，上面四张图的“叔”、“1”、“2”、“3”结点有可能为黑哨兵结点。
　　其实红黑树的插入操作不是很难，甚至比AVL树的插入操作还更简单些。但删除操作就远远比AVL树复杂得多，下面就介绍红黑树的删除操作。 　　

HashMap源码解析

主要讲解红黑树的平衡插入

//LinkedHashMap.Entry<K,V>继承自HashMap.Node<K,V> 
 static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {

     TreeNode<K,V> parent;//parent阴阳记录父亲节点

     TreeNode<K,V> left;//left、right其中一个记录叔叔节点

     TreeNode<K,V> right;

     TreeNode<K,V> prev;  // needed to unlink next upon deletion

     boolean red; //记录节点的颜色

     TreeNode(int hash, K key, V val, Node<K,V> next) {

         super(hash, key, val, next);

     }
 
     /**

      * 将链表转化为红黑树

      */

     final void treeify(Node<K,V>[] tab) {

         TreeNode<K,V> root = null;

         //遍历链表,x代表需要插入的节点

         for (TreeNode<K,V> x = this, next; x != null; x = next) {

             next = (TreeNode<K,V>)x.next;

             x.left = x.right = null;

             if (root == null) {//树为空直接插入节点，并且节点颜色变为黑色

                 x.parent = null;

                 x.red = false;

                 root = x;

             }

             else {

                 K k = x.key;

                 int h = x.hash;

                 Class<?> kc = null;

                 //查找新节点在红黑树上的位置

                 for (TreeNode<K,V> p = root;;) {

                     //dir记录向左走还是向右走 ph 记录当前节点的hash值

                     int dir, ph;

                     K pk = p.key;


                     if ((ph = p.hash) > h)

                         dir = -1;

                     else if (ph < h)

                         dir = 1;

                     else if ((kc == null &&

                               (kc = comparableClassFor(k)) == null) ||

                              (dir = compareComparables(kc, k, pk)) == 0)

                         //哈希值相等时比较Key的大小

                         dir = tieBreakOrder(k, pk);



                     TreeNode<K,V> xp = p;

                     //如果下一步需要到达的位置是null，就可以安放新节点

                     if ((p = (dir <= 0) ? p.left : p.right) == null) {

                         x.parent = xp;

                         if (dir <= 0)

                             xp.left = x;

                         else

                             xp.right = x;

                         //插入红黑树，并且保证红黑树的特性不被破坏

                         root = balanceInsertion(root, x);

                         break;

                     }

                 }

             }

         }

         moveRootToFront(tab, root);

     }


     static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,

                                                 TreeNode<K,V> x) {

         x.red = true;

         //xp表示x的父节点 xpp表示x的祖父节点 xppl、xppr表示x叔叔节点

         for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {

             //根节点直接变为黑色
             if ((xp = x.parent) == null) {
                 x.red = false;
                 
                 return x;
                 
             }

             //父亲为红色或者父节点为根节点 直接插入红色新节点

             else if (!xp.red || (xpp = xp.parent) == null)

                 return root;

             //父亲节点是左节点

             if (xp == (xppl = xpp.left)) {

            //父亲节点和叔叔节点是红色，则叔叔和父亲变为黑色，祖父变为红色

                 if ((xppr = xpp.right) != null && xppr.red) {

                     xppr.red = false;

                     xp.red = false;

                     xpp.red = true;

                     x = xpp; //祖父节点作为新节点，继续平衡之路

                 }

                 else {

                     if (x == xp.right) {

                         root = rotateLeft(root, x = xp);

                         xpp = (xp = x.parent) == null ? null : xp.parent;

                     }

                     if (xp != null) {

                         xp.red = false;

                         if (xpp != null) {

                             xpp.red = true;

                             root = rotateRight(root, xpp);

                         }

                     }

                 }

             }

             else { //父亲节点是右节点
             //父亲节点和叔叔节点是红色，则叔叔和父亲变为黑色，祖父变为红色

                 if (xppl != null && xppl.red) {

                     xppl.red = false;

                     xp.red = false;

                     xpp.red = true;

                     x = xpp;//祖父节点作为新节点，继续平衡之路

                 }

                 else { //父亲节点和叔叔节点是红色

                     if (x == xp.left) {

                         root = rotateRight(root, x = xp);

                         xpp = (xp = x.parent) == null ? null : xp.parent;

                     }

                     if (xp != null) {

                         xp.red = false;

                         if (xpp != null) {

                             xpp.red = true;

                             root = rotateLeft(root, xpp);

                         }

                     }

                 }

             }

         }

     }