数组排成最小的数

发表于   |   分类于   |  

题目

　　输入一个正整数数组，每个元素都不相等，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如数组{3，32，321},则打印出这3个数字能排成的最小数字321323.（《剑指Offer》P177）

　　贪心算法的题目，找到解决办法不能，难得是给出正确性证明。书中给出了证明，前半段讲的很好，不过后半段不是很满意。 　　

解题思路

1）将数组中所有数字转化为字符串，组成新的数组Str
2）对所有字符串排序。 return Str[i]+Str[j]<Str[j]+Str[i]

源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public static class MinStringComparator implements Comparator {
     @Override
     public int compare(Object o1, Object o2) {
         return (o1.toString() + o2.toString()).compareTo(o2.toString() + o1.toString());
     }
 }

 public static void main(String[] args) {
     Integer[] arr = new Integer[]{3, 32, 321};
     List<Integer> list = Arrays.asList(arr);
     Collections.sort(list, new MinStringComparator());
     StringBuilder stringBuilder = new StringBuilder(100);
     for (Integer e : list) {
         stringBuilder.append(e);
     }
     System.out.println(stringBuilder.toString());

正确性证明

排序关系有效性证明

一个有效的比较规则一定满足自反性、对称性和传递性。
1）自反性：显然有 aa = aa,所以a等于a。
2）传递性：如果a小于b，则abab,因此b大于a。
3）传递性：假设a小于b，ab<ba. b小于c，bc<cb
a的十进制为m位，b的十进制为n位，c的十进制为k位

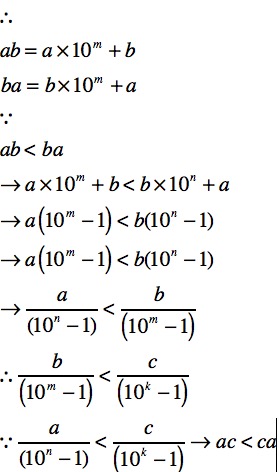
因此 a小于b，b小于c，a必定小于c

最终证明

排序关系证明是很重要的前提。正面证明很困难，使用反证法。

1
2
3
4
5
6
7
假设存在一个序列A小于序列B。
1）假设B[i] = A[j],我们可以一直向前或者向后移动B[i]直到B[i]到达位置j。B序列中的每一个元素都按照这种方法移动即可得到A序列。
2）现在我没减缓这个移动过程，每次只移动一个特定的元素B[i]一步直到B[i]到达位置j，而且一次只移动一步。可就是说经过一次移动序列B(0)：B[0]...B[i-1]B[i]...变为B(1):[0]...B[i]B[i-1]...。 B(l)代表序列B经历过l次移动。
3)因为B[i-1]B[i]<B[i]B[i-1]（这一点需要排序关系证明的支持才能成立），所以B[0]...B[i-1]B[i]...<[0]...B[i]B[i-1]...
4）因为B[i]B[i+1]<B[i+1]B[i]（这一点需要排序关系证明的支持才能成立），所以B[0]...B[i-1]B[i]...<[0]...B[i]B[i-1]...
5)因为B(0)<B(1)<B(2)<...<B(x)=A(0)，所以B<A
这与题设不相符，所以假设不成立。也就是说A是最小的序列